 visiteurs
visiteurs
Rapport 
Qualités
de vol de l'avion souple
Influence de la souplesse voilure sur le foyer
Dominique
BLANC Rodolphe GOURSEAU |
P.I.R. Long
X
PROMOTION 2005
SUPAERO-ONERA
Remerciements
Nous remercions Jean-Luc Boiffier et Clément Toussaint pour nous avoir guidés
et soutenus tout au long de ce projet de recherche.
Nous soulignons également la contribution essentielle des travaux d'Élodie
Roux et de Marco Adurno à notre étude.
Table des matières
De même que n'importe quelle structure soumise à une sollicitation, une aile d'avion
se déforme sous l'action des forces aérodynamiques. Ainsi, même si les mécaniciens
des structures tentent de minimiser leurs effets, portance et traînée ont une
incidence sur l'aspect d'une aile qui, portant, n'a plus en l'air la forme qu'elle
avait au sol.
Un cisaillement dans la direction de la largeur d'une poutre la déforme moins
que s'il lui est appliqué selon son épaisseur. Si on suppose en plus que l'aile
d'avion a une bonne finesse (portance supérieure d'un ordre de grandeur à la traînée),
on peut supposer que l'effet principal des contraintes aérodynamiques est celui
de la portance.
On s'attend alors logiquement à un déplacement vertical de l'aile sous l'effet
de sa souplesse. Mais, par un effet géométrique, ce déplacement induit également
une diminution de l'incidence locale de l'aile. Cela a pour conséquence de faire
avancer le foyer de l'avion. Ce phénomène peut être dangereux si le foyer passe
devant le centre de gravité de l'avion. L'avion est alors instable, c'est-à-dire
que soumis à une rafale qui augmenterait son incidence, la somme des moments tendrait
à faire augmenter cette incidence, et l'avion deviendrait incontrôlable. Mais
sans aller jusqu'à cette situation, le déplacement du foyer a une influence sur
la maniabilité de l'avion. À deux masses différentes (ie pour deux déformations
différentes de la voilure) mais pour le même ordre du pilote, l'avion régira différemment.
On comprend alors l'intérêt de pouvoir prévoir le déplacement du foyer d'un avion.
Notre étude, qui allie structures, aérodynamique et géométrie, a pour objectif
de retrouver cet effet par la théorie, de le quantifier et de comparer nos résultats
théoriques aux données disponibles. Pour rendre nos développements plus concrets,
nous les appliquerons au cas de l'Airbus A300-600.
Dans cette partie, nous définissons les variables, les notations ainsi que le
modèle d'atmosphère utilisé pour la calcul de la masse volumique de l'air à l'altitude
de croisière, le modèle géométrique d'aile (purement trapézoïdale) et le type
de répartition de portance que nous utiliserons.
2.1 Notations

Figure 2.1: Repère avion et axe élastique
On considère le repère avion canonique Oxyz et on introduit l'axe Oη
élastique de l'aile. L'angle entre Oy et Oη est l'angle de flèche
φ.
On introduit une variable adimensionnée y
suivant l'axe Oy. On a alors: y=y b/2.
η est une variable adimensionnée par b/2 cos(φ).
On utilise les notations suivantes:
- φ: angle de flèche;
- b: envergure des deux ailes;
- h:
coefficient permettant de ne considérer que la hauteur du longeron sans la
peau, rapport entre la hauteur effective du longeron et l'épaisseur de l'aile;
- er: épaisseur relative du profil,
rapport entre l'épaisseur et la corde;
- cemp: corde à l'emplanture;
- cma: corde moyenne aérodynamique;
- ε: effilement, rapport entre la corde à l'extrémité
et la corde à l'emplanture;
- λ: allongement de l'aile, rapport entre le carré
de l'envergure et la surface alaire;
- Sa: surface alaire;
- E: module d'Young du matériau du caisson;
- MMTOW: masse maximale au décollage;
- V: vitesse de croisière;
- nz: facteur de charge extrême;
- g: accélération de la pesanteur;
- σ = −3.10−3
E: contrainte extrême en compression du matériau du caisson;
- ρ: masse volumique locale de l'air;
- Czα: gradient
de coefficient de portance;
- v: déformation transversale suivant Oz
locale de l'aile en mètres.
2.2 Masse volumique de l'air
On considère le modèle standard de l'atmosphère pour évaluer la masse volumique
de l'air à une altitude donnée ζ.
Les valeurs références sont:
ρ0 = 1.225 kg.m−3
(2)
ζ0 = 9.103 m
(3)
Ainsi à une altitude de 10000 m, la masse volumique de l'air
vaut:
ρ~0.403 kg.m−3
(4)
2.3 Hauteur de caisson
On fait l'hypothèse que la corde varie linéairement en fonction de η:
c=cemp (1+(ε−1) η)
(5)
Cette corde est la longueur d'une section d'aile prise dans le sens de l'écoulement
amont de l'air. La corde c est donc parallèle à l'axe Ox, ou encore
perpendiculaire à Oy.
On peut aussi exprimer aussi la corde en fonction de y:
On suppose de plus que l'épaisseur relative er et le
coefficient h sont constants
sur toute l'aile. Ainsi la hauteur du caisson varie linéairement en fonction de
la corde et s'exprime par 1:
| h= |
|
er c= |
|
er cemp (1+(ε−1) η)
(7) |
On peut alors mettre en évidence les relations suivantes:
| cma= |
|
|
∫ |
|
c(y) d y =cemp |
|
(8) |
Sa=b cma
(9)
b=λ cma (11)
2.4 Force de portance
On considère un cas simplifié où la force de portance varie proportionnellement
avec la corde. On choisit donc une force linéique Fη du
type:
Fη=K c(η) (12)
Il s'agit d'une force linéique par unité de longueur suivant l'envergure.
K est une constante qui s'interprète physiquement comme une portance surfacique.
L'égalité de l'accélération (produit du facteur de charge extrême et du poids)
et de la portance à la rupture Fextr (cas dimensionnant
pour les semelles du caisson) pour une seule aile permet de déterminer la valeur
de K:
| Fextr= |
|
|
∫ |
|
K c(η) cos(φ) dη= |
|
(13) |
Le terme c(η) cos(φ) provient du fait qu'il faut projeter
la corde selon un axe perpendiculaire à l'axe d'intégration qui est ici l'axe
élastique Oη (voir figure 2.2).

Figure 2.2: Corde réelle et corde projetée
Le terme b/2 cos(φ) vient du fait que η est une grandeur adimensionnée
et que l'intervalle d'intégration est physiquement [ 0 ; b/2 cos(φ) ].
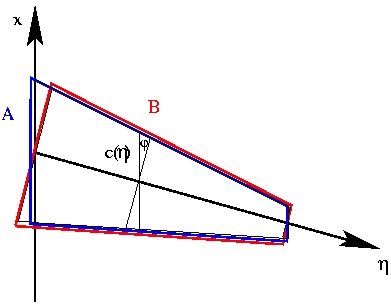
Figure 2.3: Surface de l'aile et surface d'intégration
En intégrant de cette manière, on n'intègre pas sur la forme véritable A
de l'aile, mais sur une forme B différente aux extrémités (comme le montre
la figure 2.3). En fait, un calcul simple d'aire de trapèzes
montre que ces deux surfaces sont égales.
Après calcul, on obtient la forme suivante pour la force linéique de portance:
| K= |
| 2 MMTOW nz g |
|
| b cemp (ε+1) |
|
(14) |
- 1
- Élodie Roux, Méthodes de masse voilure [1],
p. 57
Chapitre 3 Calcul du moment
quadratique
Pour calculer la déformation de l'aile, les équations de structures nécessitent
la connaissance du moment quadratique du caisson. Pour cela, nous avons besoin
de ses caractéristiques. N'ayant pas accès aux valeurs-constructeur des sections
des semelles du caisson, nous les dimensionnons pour supporter les charges extrêmes.
3.1 Moment de flexion de la
force de portance
Pour l'aile tribord, on calcule d'abord le moment de flexion de la force de portance
Fη=K c(η) exercé par la portion située
à droite de η sur la portion à gauche ou encore le moment en η de toute
la portance qui s'exerce à droite de η:
| MF=( |
|
)2 |
∫ |
|
(1− |
|
) [K c( |
|
) cos(φ)] d |
|
(1) |
Là encore il faut voir le coefficient K comme une portance surfacique.
Comme on effectue l'intégration dans la direction de l'axe élastique Oη,
l'élément de surface à considérer est: c(η) cos(φ) dη.
Comme pour le calcul de la force de portance, la surface d'intégration ne correspond
pas à la forme réelle de l'aile (voir figure 2.2). L'intégration
suivant la surface B est plus naturelle et le résultat obtenu est le même
que celui obtenu avec la surface A. Tout calcul fait, on obtient le résultat
suivant:
| MF= |
| b MMTOW nz g |
|
| 12 (ε+1) cos(φ) |
|
(1−η)2 (ε+2 [1+(ε−1) η])
(2) |
Remarquons la dépendance en 1/cos(φ) qui fait augmenter le moment avec la
force. Cette évolution se comprend lorsque l'on voit qu'augmenter φ revient
à augmenter la longueur de la poutre sans changer l'envergure de l'aile.
3.2 Moment quadratique d'une
section
En compression, la surface de la semelle extrados est dimensionnée selon le critère 1:
En utilisant les résultats précédents, on obtient:
| SE=− |
| b MMTOW nz g |
|
| 12 (ε+1) σ |
|
er cemp cos(φ) |
|
|
|
| (1−η)2 (ε+2 [1+(ε−1) η]) |
|
| 1+(ε−1) η |
|
(4) |
Nous dimensionnons la semelle intrados par la formule simple suivante qui représente
bien la réalité:
La surface extrados doit assurer la tenue de l'aile pour un facteur de charge
de 2.5× 1.5. La surface intrados doit, elle, tenir pour un facteur de charge de
−1× 1.5. Il est donc raisonnable de prendre un rapport de section SE/SI
égal au rapport des facteurs de charge |2.5× 1.5/−1× 1.5|=2.5.
Le moment quadratique est donné par 2:
Le résultat du calcul du moment quadratique est le suivant:
| Iy=− |
|
(1−η)2 (ε+2 [1+(ε−1) η])
(1+(ε−1) η) (7) |
- 1
- Élodie Roux, Modèle de Masse Voilure [1],
p. 55
- 2
- Élodie Roux, Méthodes de masse voilure [1],
p. 52
Chapitre 4 Déplacement
du foyer
L'objet de ce chapitre est d'estimer l'avancement du foyer dû à la souplesse de
l'aile. Pour cela, il nous faut connaître la déformation de l'aile. Celle-ci va
modifier la répartition de la portance ainsi que le moment de tangage et le point
d'application de la résultante aérodynamique.
4.1 Dimensionnement et vol
Le calcul du moment quadratique est effectué pour le facteur de charge extrême
nz=2.5× 1.5=3.75 qui est dimensionnant pour les semelles.
En revanche, pour la suite on se place dans le cas du vol de croisière
où nz=1.
Les expressions littérales de la force de portance et de son moment de flexion
(déterminés pour un facteur de charge quelconque) sont a fortiori valables
en prenant cette nouvelle valeur de facteur de charge.
4.2 Loi de déformation
La loi de déformation de l'aile v(η) est donnée en fonction du moment
de portance à nz=1, du moment quadratique de dimensionnement(nz=3.75)
et du module d'Young E.
Le terme (2 cos(φ)/b)2 vient du fait que η est
une variable adimensionnée par b/2 cos(φ).
Après calcul, on obtient:
Une première intégration sur [0;η] avec la condition ∂ v/∂η(0)=0
donne:
Une deuxième intégration sur [0;η] avec la condition v(0)=0 donne le
résultat final:
| v(η)=− |
|
|
| 1+ [1+(ε−1) η](ln[1+(ε−1)
η]− 1) |
|
| (ε−1)2 |
|
(4) |
La flèche est maximale en η=1 et la valeur maximale 1
est:

Figure 4.1: Allure de la flèche v en fonction de
η
4.3 Loi d'incidence

Figure 4.2: Variation d'incidence Δα
Le fait que l'axe élastique ne soit pas perpendiculaire à l'écoulement (et donc
à la corde aérodynamique) entraîne que les extrémités d'une corde n'appartiennent
pas à la même section élastique. Par conséquent, la flexion de l'aile crée dans
l'axe de la corde une incidence locale supplémentaire Δα(η) qui
dépend de la flexion v(η). Ainsi, comme le montre la figure 4.2,
on a:
| tan(Δα)= |
| v[η− |
|
|
|
sin(φ)]− v[η+ |
|
|
|
sin(φ)] |
|
|
| c(η) |
|
(6) |
Le terme en 2 cos(φ)/b associé au terme c(η) est indispensable
car la variable η est adimensionnée.
Dans la suite, on pose:
Ce qui conduit à:
qui est équivalent à:
En effectuant un développement limité au premier ordre 2
en η, la variation d'incidence due à la flexion de l'aile suit la loi:
On linéarise aux petits angles:
| Δα=− |
|
sin(φ) cos(φ) v'(η) (11) |
On obtient finalement:

Figure 4.3: Allure de la variation d'incidence Δα
en fonction de η
4.4 Avancement du foyer
On vient de mettre en évidence l'apparition d'une variation d'incidence due à
la souplesse de l'aile. Celle-ci va donc perturber la répartition linéique de
portance Fη calculée en vol de croisière pour une aile rigide,
et va modifier la position du foyer.
Dans un premier temps, on s'intéresse à la portance linéique de l'avion rigide
en vol de croisière à la vitesse V.
Elle s'exprime par:
| (Fη)R=Knz=1 c(η)= |
|
(1+(ε−1) η) (13) |
La portance totale d'une aile est donc:
| FR= |
|
|
∫ |
|
Knz=1 c(η) cos(φ)
d η= |
|
(14) |
En raison de la flèche de l'aile, le moment de tangage associé a deux composantes:
l'une suivant Ox et l'autre suivant Oy. Or seule la contribution
suivant Ox influe sur la position longitudinale du foyer (par symétrie
de l'avion, les composantes suivant Oy des deux ailes sont opposées et
s'annulent). On calcule donc le moment de tangage de la portance rigide projeté
sur l'axe Ox.
| MR=sin(φ) ( |
|
)2 |
∫ |
|
η Knz=1 c(η) cos(φ)
d η (15) |
soit
On note xR la distance entre l'origine O (point
d'intersection de l'axe Ox et de l'axe élastique Oη) et la position
du foyer rigide. Le point O est un point de la corde à l'emplanture. La
prise en compte du diamètre du fuselage n'est pas nécessaire dans le problème
du tangage (symétrie de l'avion par rapport à Ox). On a:
On peut adimensionner par la corde à l'emplanture ou par la corde moyenne aérodynamique
la position du foyer dans le cas statique. On obtient alors:
Dans un deuxième temps, on calcule la portance de l'avion souple ce qui nécessite
de connaître la portance linéique. On peut décomposer cette portance linéique
en deux contributions: la première est celle due à l'avion rigide, et la deuxième
provient de la variation locale d'incidence due à la flexion de l'aile. Cela s'écrit:
| (Fη)S= |
|
[(Fη)R+ |
|
Czα c(η) Δα]
(20) |
Le coefficient Γ est ajusté de manière à équilibrer la portance totale et
le poids de l'avion:
Pour cela, on intègre la formule précédente:
On obtient alors l'expression de Γ:
On calcule ensuite la composante suivant Ox du moment de tangage associé
à la force FS:
| |
|
| |
| 5pt+ |
| 7 b3 ρ V2 σ Czα sin(φ)tan(φ) |
|
|
|
|
| 6 ε2 (2ε−3) ln(ε)−(ε−1)(4ε2−5ε−5) |
|
| (ε−1)3 |
|
|
|
(24) |
En introduisant cma, on a:
| |
|
| |
| 5pt+ |
|
|
| 6 ε2 (2ε−3) ln(ε)−(ε−1)(4ε2−5ε−5) |
|
| (ε−1)3 |
|
ρ V2 cma3 |
|
|
(25) |
Puis on obtient la position du foyer de l'avion souple:
Le déplacement du foyer peut alors être évalué par:
4.5 Application numérique
Pour un Airbus A300-600 3,
on a:
- φ=28
- b=39.6 m
- h=0.93
- er=0.11
- cemp=10 m
- ε=0.29
- E=2.1011 Pa
- MMTOW=165000 kg
- V=245 m.s−1 (M=0.82)
- nz=2.5 × 1.5 = 3.75
- g=9.81 m.s−2
- σ=−3.10−3 E=−6.108 Pa
- ρ=0.403 kg.m−3
(à une altitude de 10000 m)
- Czα=5
Après calcul, on obtient:
soit
On obtient finalement un avancement du foyer dans le cas de statique de:
soit
Δ x=0.27 m (31)
- 1
- Pour un Airbus A300-600, cette valeur vaut numériquement
0.96 m [voir section 4.5].
- 2
- On commet une erreur de moins de 1% sur toute l'envergure
du profil en ne conservant que le premier terme dans le développement limité,
ce qui justifie cette approximation.
- 3
- Élodie Roux, Modèle de masse voilure [1],
p. 30-32
Le résultat présenté au chapitre précédent a été obtenu en utilisant certaines
hypothèses dont il faut vérifier la validité.
Nous comparerons également notre résultat numérique à la donnée-cons-tructeur.
5.1 Choix de la répartition
de portance
5.1.1 Corde linéaire
On a choisi de représenter l'aile comme un trapèze. Ce choix de forme ne correspond
pas à l'aspect réel d'une aile. En effet, afin de ménager de l'espace pour le
mécanisme du train d'atterrissage, le bord de fuite des ailes de la plupart des
avions de transport civil présente une cassure que nous n'avons pas prise en compte
(voir figure 5.1). Celle-ci se traduit par un changement
de flèche du bord de fuite (flèche nulle à l'emplanture).
Figure 5.1: Airbus A300 cassure du bord de fuite
Cette cassure invalide notre hypothèse de corde linéaire. Du même coup, la surface
alaire réelle de l'avion n'est pas celle qu'on obtient par notre calcul. Toutefois
la différence relative entre ces deux aires est inférieure à 1.5%, ce qui justifie
cette approximation. En outre, les déformations de l'aile ont surtout lieu à son
extrémité, et c'est donc cette partie de l'aile qui influence le plus le déplacement
du foyer.
5.1.2 Portance proportionnelle
à la corde
Dans notre développement, pour simplifier les calculs, nous avons supposé que
la portance locale était proportionnelle à la corde.
Il existe d'autres modèles plus réalistes de répartition de portance, comme la
répartition elliptique. Cependant on ne peut pas mener des calculs de manière
analytique avec ce type de modèles.
Nous avons aussi négligé les contributions du fuselage et de l'empennage alors
qu'ils participent également au moment de tangage et au déplacement du foyer par
leur souplesse [2].
En tout état de cause, il nous est difficile d'estimer l'erreur que nous commettons
en faisant cette hypothèse.
5.2 Modèle de structure
5.2.1 Semelles du caisson
Nous avons dimensionné la surface de la semelle extrados du caisson en considérant
qu'elle ne travaillait qu'en compression. Le dimensionnement pourrait être amélioré
en appliquant le modèle plus précis développé par Élodie Roux [1].
Pour la semelle intrados, nous avons raisonné sur les facteurs de charge extrêmes
ce qui a certainement introduit une erreur supplémentaire.
Ces deux approximations disparaîtraient si l'on avait accès aux données-constructeur.
5.2.2 Influences
Les hypothèses utilisées pour déterminer les surfaces des semelles du caisson
ont un impact direct sur l'estimation du moment quadratique.
Puis on a introduit la déformation de l'aile en considérant que le problème se
ramenait à celui d'une poutre 1D. Là encore la validité de ce choix est discutable
compte tenu des dimensions du caisson.
Toutes les petites approximations signalées se cumulent, et il nous est malheureusement
difficile de connaître l'ordre de grandeur des erreurs qu'elles introduisent.
La seule façon de s'affranchir de ces approximations serait d'avoir accès aux
données-constructeur (surface de la semelle, mesure directe en essai en vol de
la déformation de l'aile...).
5.3 Simplification de la statique
de l'avion
souple
Lors du calcul de l'avancement du foyer, nous avons d'abord étudié le cas de l'avion
rigide auquel nous avons ajouté une perturbation (variation locale d'incidence)
pour obtenir le cas de l'avion souple.
Ce raisonnement aurait fourni une portance inférieure au poids si nous n'avions
pas normalisé la portance totale.
Pour être rigoureux, il aurait fallu redéfinir l'équilibre de l'avion en utilisant
les angles d'incidence. On aurait alors des incidences différentes dans les cas
rigide et souple (l'incidence dans le cas souple étant plus faible que celle dans
le cas rigide).
Conformément à l'équation 1, si l'on veut que F soit
constante alors que α diminue, il faut que V augmente (toutes choses
égales par ailleurs).
D'un point de vue quantitatif, il est impossible d'avoir accès aux paramètres
de vol de l'avion rigide puisque tous les avions sont souples.
[LO]Synthèse
Le déplacement que nous avons calculé n'est dû qu'à la souplesse des ailes.
Comme nous l'avons dit précédemment, fuselage et empennage contribuent également
à la portance et leur souplesse participe à l'avancement du foyer. On peut prendre
en compte cet incrément en reprenant les résultats d'une étude précédente de
l'ONERA 1 qui évalue cette
contribution à l'avancement à 0.99% de la cma. On l'ajoute
alors à notre résultat (4.13%). On obtient finalement un avancement du foyer
de l'avion de 5.12% de la cma.
Pour l'avion complet, par une méthode statistique, Airbus 2
évalue l'avancement du foyer à 7.27%.
| |
Déplacement du foyer en pourcentage de la cma
|
| Modèle empennage-fuselage ONERA |
-0.99 |
| Modèle voilure présenté |
-4.13 |
| Total empennage-fuselage-voilure |
-5.12 |
| Modèle statistique Airbus (avion complet) |
-7.27 |
L'ordre de grandeur de notre résultat est satisfaisant compte tenu de la simplicité
du raisonnement que nous avons suivi.
Avec des modèles rustiques, on a réussi à approcher l'avancement réel du foyer.
En les approfondissant, on peut donc sans doute représenter la réalité avec une
meilleure fidélité. De plus, la prise en compte des effets dynamiques devrait
certainement améliorer l'estimation du déplacement du foyer.
- 1
- section 3.3 de la référence [2]
- 2
- section 3.3 de la référence [2]
Références
- [1]Élodie
Roux, Modèle de Masse Voilure, thèse SUPAERO - ONERA, 2003
- [2]Marco
Adurno, L'avion souple: approche analytique — avions de transport
civil, stage long SUPAERO - ONERA, 2003-2004
Ce document a été traduit de LATEX
par HEVEA
 page d'accueil
page d'accueil
visiteurs

 Figure 4.1: Allure de la flèche v en fonction de η
Figure 4.1: Allure de la flèche v en fonction de η